NILAI MUTLAK ~ PENDIDIKAN MATEMATIKA DASAR

Adalah jarak antara bilangan yang dimaksud dengan nilai nol. Nilai mutlak di tandai dengan lambang | |. Untuk x sebagai bilangan real, maka x didefinisikan sebagai berikut :

$\mid X\mid=\left\{\begin{matrix} X& jika & x\geqslant 0 \\ -X & jika & x< 0 \end{matrix}\right.$

Dimana |x| adalah nilai positif dari nilai –x dan x.

Agar lebih jelas, kita akan merancang konsep harga mutlak dari suatu bilangan real x hubungannya dengan konsep jarak dari x ke titik 0.

• Jarak titik P = 3 ke titik C dan titik A

• Jarak titik Q = 3 ke titik C dan titik B

• Untuk $a> 0$ , jarak titik A =a ke titik C = 0 adalah a – 0 = a

• Untuk $b< 0$ , jarak titik B = a ke titik C = 0 adalah a – b = - b

• Untuk $a> 0$ , jarak dari titik C = 0 ke titik C adalah 0

2. Persamaan nilai mutlak

Adapun sifat – sifat dari nilai mutlak tersebut dapat didefinisikan sebagai berikut :

a. |a b| = |a| . |b|

b. |a/b| = |a| / |b|

c. |a + b| ≤ ||a| + |b||

d. |a - b| ≥ ||a| - |b||
e. $\sqrt{x}^{2} = \mid x\mid$

f. $\mid x\mid ^{2}=x^{2}$

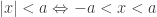
g. $\left | x \right |< a\Leftrightarrow -a< x< a$

h. $\mid x\mid> a\Leftrightarrow x< -a$ atau $x> a$

3. Pertidaksamaan nilai mutlak
Adapun sifat – sifat dari pertidaksamaan adalah sebagai berikut :
Untuk x,y dan c adalah bilangan real dan c $>$ 0, maka :
a. $\mid x\mid \geq 0$
b. $\mid x+y\mid \leq \mid x\mid +\mid y\mid$
c. $\mid x-y\mid \leq \mid x\mid -\mid y\mid$
d. jika $x< y$ maka $x^{2}< y^{2}$
e. $\mid x\mid \leq c\Leftrightarrow -c\leq x\leq c$
f. $\mid x\mid \geq c\Leftrightarrow x\leq -k$ atau $x\geq c$

Contoh Soal

1. Tentukan himpunan penyelesaian dari | x + 3 | + | 3x + 6 | = 10
Penyelesaian :
Untuk menentukan nilai soal diatas, kita perlu membagi setiap bentuk aljabar nilai mutlaknya :

$x+3=\left\{\begin{matrix} (x+3) &jika &x\geq -3 \\ -(x+3)&jika & x< -3 \end{matrix}\right.$
$3x-6=\left\{\begin{matrix} (3x-6) &jika &x\geq 2 \\ -(3x-6)&jika & x< 2 \end{matrix}\right.$
jika dilihat dari gambar, bentuknya sebagai berikut :

Dari hasil pembagian diatas, masing - masing dapat diperoleh 3 garis bilangan yaitu :

$x< -3\cdots -3\leq x< 2\cdots x\geq 2$

Selanjutnya kita uji ketiga bagian tersebut.

$x< -3$

$-(x< -3)+(3x-6)=10\Rightarrow -x-3+3x-6=10\Rightarrow x=\frac{1}{2}$ (tidak memenuhi)

$-3\leq x< 2$

$(x+3)+-(3x-6)=10\Rightarrow x+3-3x+6=10\Rightarrow x=-\frac{1}{2}$ (memenuhi syarat)

$x> 2$

$-(x< -3)+(3x-6)=10\Rightarrow -x-3+3x-6=10\Rightarrow x=\frac{1}{2}$ (tidak memenuhi)

Jadi himpunan penyelesaiannya adalah $-\frac{1}{2}$

2. Tentukan himpunan penyelesaian dari $\mid 2x+7\mid \leq \mid x+3\mid$
Penyelesaian :
$\mid 2x+7\mid \leq \mid x+3\mid \Leftrightarrow (2x+7)^{2}\leq (x+1)^{2}$
   $4x^{2}+28x+49\leq x^{2}+6x+9$
   $4x^{2}+28x+49-x^{2}+6x+9\leq 0$
   $3x^{2}-22x+40\leq 0$
$(3x-10)(x-4)\leq 0$
$x=\frac{10}{3}\, atau\, x=4$

jadi himpunan penyelesaiannya adalah $\frac{10}{3}\leq x\leq 4$

Artikel lebih lanjut mengenai nilai mutlak dapat dilihat pada postingan " Penting Diketahui Untuk Menyelesaikan Permasalahan Nilai Mutlak "

PENDIDIKAN MATEMATIKA DASAR

NILAI MUTLAK

0 komentar:

Post a Comment