Konsep eksponen dan algoritma sangat berperan penting dalam menyelesaikan masalah - masalah dalam kehidupan sosial misalnya dalam masalah aritmatika, proses kimia dan fisika. Dalam bab ini akan diuraikan bagaimana konsep dari ekponensial dan algoritma tersebut.
- Eksponen (Pangkat)
Sifat dari bilangan eksponen tersebut antara lain :
- Jika suatu bilangan dipangkatkan dengan 0, maka hasilnya adalah 1. Contoh :
- Jika suatu bilangan dipangkatkan dengan 1, maka hasilnya adalah bilangan itu sendiri. Contoh :
- Jika suatu bilangan dipangkatkan dengan bilangan negatif, maka berlaku bentuk sebagai berikut :
- Jika suatu bilangan berpangkat dikalikan dengan bilangan berpangkat lain, maka pangkat dari setiap bilangan dijumlahkan. Contoh :
- Jika suatu bilangan berpangkat dibagi dengan bilangan berpangkat lain, maka pangkat dari setiap bilangan dikurangkan. Contoh :
- Jika suatu bilangan berpangkat pecahan, dapat dituliskan sebagai berikut :
- Jika suatu bilangan berpangkat di kuadratkan dengan suatu bilangan, dapat dituliskan sebagai berikut :
Contoh soal :
- Diketahui bilangan sebagai berikut :
tulislah dalam bentuk yang lebih sederhana !
Pembahasan :
^{7}x(4x4)^{3}}{(4x3)^{2}}=\frac{(6)^{7}x(4)^{3}}{(3)^{2}}=\frac{(24)^{7+3}}{(3)^{2}}=\frac{(24)^{10}}{(3)^{2}})
2. Hitunglah nilai x dari persamaan eksponen berikut ini :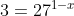
Pembahasan :
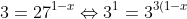}\Leftrightarrow1=3(1-x)\Leftrightarrow1=3-3x\Leftrightarrow3x=2\Leftrightarrow&space;x=\frac{3}{2})
- Logaritma
Prinsip dasar daro Logaritma itu sendiri adalah kebalikan dari eksponen, yaitunya merubah suatu bilangan menjadi suatu bilangan berpangkat (eksponen). Jika 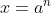 maka
maka 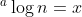 . Dengan demikian, hubungan antara eksponen dengan logaritma dapat dinyatakan sebagai berikut :
. Dengan demikian, hubungan antara eksponen dengan logaritma dapat dinyatakan sebagai berikut :
Keterangan :
a = basis
x = bilangan yang dilogaritma
n = hasil logaritma
Sedangkan untuk sifat - sifat dari logaritma itu adalah sebagai berikut :
Keterangan :
a = basis
x = bilangan yang dilogaritma
n = hasil logaritma
Sedangkan untuk sifat - sifat dari logaritma itu adalah sebagai berikut :
- Jika a dan x mempunyai nilai yang sama, maka hasil nya adalah 1. Contoh :
- Jika x = 1, maka hasil dari logarima adalah nol. Contoh :
- Jika x merupakan bilangan eksponen, maka hasil logaritma adalah bilangan eksponen tersebut dikalikan dengan persamaan logaritma pertama. Contoh :
- Jika x merupakan perkalian, maka hasil logaritma adalah penjumlahan dari logaritma x. Contoh :
- Jika x merupakan pembagian, maka hasil logaritma adalah pengurangan dari logaritma x. Contoh :
- Jika a dan x merupakan bilangan eksponen, maka hasil logaritma adalah pangkat x dibagi pangkat a dikali dengan logaritma x. Contoh :
- Untuk kasus perkalian dua atau lebih logaritma,jika x dari persamaan logaritma pertama sama dengan a dari persamaan logaritma kedua, maka hasil logaritma adalah
. Contoh :
- Bentuk khusus:
- Rubahlah persamaan logaritma dibawah ini menjadi bentuk berpangkat :
Pembahasan :
dan
, nilai dari log 5 + log 8 + log 25 adalah : ....
Pembahasan :













0 komentar:
Post a Comment
Mohon berkomentar dengan bijak